brodata.ch

Introduction

Recent news about a significant breakthrough in the field of computer algorithms for playing the board game Go [1] reminded me about an excellent text book on the programming language LISP [2] by Christian-Michael Hamann that I read many years ago. Due to the enormous complexity of Go the game has always been regarded as a particular challenge for artificial intelligence [3]. The author thence dedicated an entire chapter of his book to the game. In order to illustrate the complexity of Go a table was presented in the introduction of chapter 8 comparing some orders of magnitude:

Table 1: Some orders of magnitude as given in [2], page 248.
10¹¹	Number of stars in our galaxy
10⁴⁰	Number of possible choices of moves in checkers (A.L. Samuel)
10¹¹⁰	Number of atoms in the universe (A. Einstein)
10¹²⁰	Number of possible choices of moves in chess (C.E. Shannon)
10⁷⁶¹	Number of possible choices of moves in Go (A.L. Zobrist)

Being completely ignorant of even the basics of astrophysics and cosmology I was quite disturbed by the fact that one can actually estimate the number of atoms in the universe. How should this be possible without seeing the whole universe, without even knowing if it is finite at all? The attribution of the number to A. Einstein, however, made it easy for me to accept my incomprehension. After having been reminded about the text book on LISP and the open question from back then I will make an attempt here to perhaps understand a little bit more.

What about the other numbers quoted in table 1 above? The estimate for the number of stars in our galaxy seems to be common knowledge. That there are around 10⁴⁰ possible choices of moves in checkers is stated in the article [4] by A.L. Samuel in the IBM Journal of Research and Development from 1959. Likewise, C.E. Shannon estimated the quoted number of possible choices of moves during a typical chess game in his essay [5] from 1950 in the Philosophical Magazine. Finally, in his conference paper [6] from 1969 A.L. Zobrist gave the rough estimate of 10⁷⁶¹ for the number of paths down the move tree for Go. Remarkably, this number does not equal 361! as it was apparently the intention in [6].

Disregarding the actual validity of the orders of magnitude as stated in table 1 I also tried to find a reference for the given number of atoms in the universe. To make it short, I failed miserably. Without much hope of getting an answer I contacted the author of [2] on that matter. To my surprise, I almost immediately got an extremely kind and benevolent reply by Chris Hamann referring me to an essay of Bill Mann [7] from where the numbers were taken. He also took the opportunity and made his very interesting review paper [3] available online where the reference to the mentioned essay of Mann’s can be found. Unfortunately, also in the essay [7] the attribution to Einstein of the estimate of 10¹¹⁰ atoms in the universe comes without any citation. With the attempt of tracking down references thus coming again to a premature end it might be indicated to have a closer look at the situation.

The Einstein static universe

Einstein’s first paper on cosmology [8] appeared in 1917, shortly after he laid the foundations of General Relativity. Due to difficulties he encountered in an attempt to specify consistent boundary conditions at spatial infinity for the gravitational field of the universe as a whole he sought to construct a simple model where such a boundary just doesn’t exist. Consequently, he took the 3-sphere as the geometry of the comoving rest space. In order to obtain a static solution, which he presumed to be evidenced by the observed small velocities of the stars, he needed to introduce a small generalization into his field equations — the famous cosmological constant.

A static universe with spatial sections of finite volume would fit perfectly both to the absolute character of the question about the number of atoms in the universe as well as to the finite answer stated in table 1. Of course, the attribution of that answer to Einstein would be obvious, too. Let’s calculate the rest mass of the pressure-free matter $M$ in Einstein’s static world. Adopting the notation in Robertson’s seminal overview article [9] it amounts to [8]

$M = 2\pi^2 R^3 \rho = \frac{\pi^2 \sqrt{32}}{c^3 \sqrt{\kappa^3 \rho}},$

where $\kappa=8\pi G/c^4$ and $\rho$ is the comoving matter density. What was a reasonable numerical value to assume for the average matter density in the universe back then? Note that it was about the time the Weltinseldebatte began to emerge which culminated in the Great Debate between H. Shapley and H. Curtis in 1920 and was finally decided by E. P. Hubble [10] in 1924. Prior to 1924 it was not clear whether the observed nebulae were objects in our own galaxy or distant galaxies by themselves. It was therefore not unreasonable to use measured densities within our galaxy as the average density of the universe. W. de Sitter, for instance, assumed $\rho=6\cdot10^{-24}\,\mathrm{g/cm^3}$ in his discussion [11] of Einstein’s static cosmological model [8]. A more erudite description of the situation can be found in the book [12] on page 158 and following. On the other hand, with the nebulae pushed to distances far outside of our own galaxy [10] with nothing much in between, Hubble already in 1926 [13] provided the much smaller estimate of $\rho=1.5\cdot10^{-31}\,\mathrm{g/cm^3}$ . This is only slightly less than what we think the average baryonic matter density is today. Using this density the mass of the Einstein static universe evaluates to $M=1.8\cdot 10^{54} \,\mathrm{kg}$ corresponding to some 10⁸¹ hydrogen atoms, not remotely what is claimed in table 1.

Einstein–de Sitter universe

After having learnt in the previous section that the number of 10¹¹⁰ atoms as ascribed to Einstein in table 1 above cannot be accounted for by the Einstein static universe even using low estimates on the average matter density an obvious thought is to look at the Einstein–de Sitter model instead. The model was introduced in a short article [14] by A. Einstein and W. de Sitter in reaction to accumulating observational evidence [15] that the universe is not static, after all. Einstein had already considered non-static universes in his discussion [16] of Friedmann models in 1931, see C. O’Raifeartaigh and B. McCann for a detailed historical account or enjoy Cormac’s noteworthy post on the story behind his article. Models of this type will be treated in a general context further down.

The Einstein–de Sitter model is spatially flat and contains, as the Einstein static universe does, matter in the form of a pressure-free ideal fluid. It is singular towards the past and grows without bound towards the future. The world radius $R(t)$ as a function of comoving time $t$ can be given explicitly as

$R(t)= \frac c{h_0} \left( \frac32 h_0 t \right)^\frac23,$

where $h_0 = h(t_0)$ is the Hubble parameter $h=R'/R$ at the present epoch $t_0$ and, without loss of generality, it is assumed that $R(t_0)=c/h_0$ . As the comoving rest space is Euclidean the volume and thus the mass of all matter in every slice $t=\mathrm{const}>0$ is not finite. A natural refinement of the question would therefore be to ask for the number of atoms in the observable universe. The observable universe is taken as that part of comoving rest space which lies in the causal past of an observer at comoving time $t_0$ , i.e. within its particle horizon. The radius of the observable universe hence is

$R_H = \frac c{h_0} P_H = \frac c{h_0} \int_0^{t_0} \frac c{R(t)}dt = \frac{2c}{h_0},$

homogeneously filled matter of density $\rho_0=3h_0^2/(\kappa c^4)$ [14] yielding a mass of

$M_H = \frac{4\pi}3 R_H^3 \rho_0 = \frac{32\pi}{\kappa c h_0}.$

When discovering the linear relationship between redshift and distance of extra-galactic nebulae [15] in 1929 Hubble proposed a value of $h_0=500\,\mathrm{km/s/Mpc}$ for the constant of proportionality. Only two years later, he and M. L. Humason [17] increased that value to $h_0=558\,\mathrm{km/s/Mpc}$ using data from much more distant nebulae. Shorty afterwards J. H. Oort [18] raised concerns about the method used by Hubble and Humason to determine distances to far away galaxies and rather estimated a value of $h_0=290\,\mathrm{km/s/Mpc}$ . The history of the numerical value of the Hubble constant remained changeful almost until the end of the 20th century. The entertaining story behind this would be worth a separate post. So let’s just presume $h_0=500\,\mathrm{km/s/Mpc}$ as a contemporary value for the purposes here and feel in good company [14]. This implies $\rho_0=4.7\cdot10^{-28}\,\mathrm{g/cm^3}$ [14] and $M_H=1.0\cdot10^{53}\,\mathrm{kg}$ corresponding to almost 10⁸⁰ hydrogen atoms, again not remotely what is claimed in table 1.

Friedmann–Lemaître models

Whilst both models considered above, the Einstein static universe and the Einstein–de Sitter model, fell short of shedding any light on the origin of the number of atoms as claimed in table 1 it is surprising that their estimated masses are of a very similar order of magnitude. Not only are the two models dynamically very different — one is static and spatially spherical with a positive cosmological constant exactly counter-balancing the mutual attraction of its material constituents while the other is ever expanding, even singular towards the past, is spatially flat and has a vanishing cosmological constant — but also the restricted focus on the region within the particle horizon of the current observer in the Einstein–de Sitter case is, of course, a source of arbitrariness. In addition, the key observational inputs used for the estimates are not closely related. In the static case it was the average matter density $\rho$ originating from galaxy counts while in the dynamic case it was the Hubble constant $h_0$ derived from the redshift–distance relation of galaxies. Both have in common just their reliance on accurate distance measurements, the Achilles’ heel of cosmology very much back then but still today, although to a lesser extent.

From what has been said above the question naturally arises as to how strongly the calculated World’s mass actually depends on the choice of the cosmological model. This shall be examined here in the context of Friedmann–Lemaître dust models. Using the current relative densities

$\Omega^0_m = \frac{\kappa c^4 \rho_0}{3h_0^2},\qquad \Omega^0_k = -\frac{kc^2}{h_0^2 R_0^2}, \qquad \Omega^0_\lambda = \frac{\lambda c^2}{3h_0^2},$

and the redshift $z=R_0/R-1$ the Friedmann equation [19,16,20] can be written in the form

$\frac{h^2}{h_0^2} = \Omega^0_m (1+z)^3 + \Omega^0_k (1+z)^2 + \Omega^0_\lambda,$

where $k \in \{1,0,-1\}$ denotes the sign of the sectional curvature of the comoving rest spaces and $R_0$ is the current World’s radius. In models with a past singularity, i.e. types O, A₁, and M₁ according to Robertson’s classification [9], the comoving radius of the region within the particle horizon of the current observer residing at the origin of comoving rest space at comoving time $t_0$ is

$P_H = \left\{ \begin{array}{lr} \sqrt{-\Omega^0_k} \min \{\Psi_H,\pi\} & (k=1) \\ \Psi_H & (k=0) \\ \sqrt{\Omega^0_k} \Psi_H & (k=-1) \end{array} \right.$

with

$\Psi_H = \int_0^{t_0} \frac c{R(t)}dt = \int_0^\infty \frac{dz}{\sqrt{\Omega^0_m (1+z)^3 + \Omega^0_k (1+z)^2 + \Omega^0_\lambda}} = 2\int_0^1 \frac{dx}{\sqrt{\Omega^0_m + \Omega^0_k x^2 + \Omega^0_\lambda x^6}}.$

The last expression in the variable $x=(1+z)^{-1/2}$ is suitable for numerical evaluation because numerical integrators tend to appreciate bounded integration intervals. As previously, in the spatially flat case it was convenient to assume $R_0=c/h_0$ without loss of generality. The mass in the observable universe is thus

$M_H = \frac1{\kappa c h_0} \frac{6\pi\Omega^0_m}{|\Omega^0_k|^{3/2}} \left(P_H - \sin P_H \cos P_H \right)$

for models with positively curved comoving rest space,

$M_H = \frac1{\kappa c h_0} 4\pi \Omega^0_m P_H^3$

for spatially flat models, and finally

$M_H = \frac1{\kappa c h_0} \frac{6\pi\Omega^0_m}{|\Omega^0_k|^{3/2}} \left( \sinh P_H \cosh P_H - P_H \right)$

for models with negatively curved comoving rest space. The models without a past singularity are of Robertson type E, A₂, and M₂ [9]. Type E is the Einstein static universe already considered. Models of type M₂ have a unique turning point at redshift $z_0$ where the Hubble parameter changes sign. They are spatially spherical and can be treated analogously to the models with positively curved comoving rest space above except that the integral with respect to redshift in the expression for $\Psi_H$ is rather the sum of the integral over the the interval $[0,z_0]$ plus over the interval $[-1,z_0]$ . What remains is type A₂. These models can be thought of as interpolating between Einstein’s static universe in the past and de Sitter space [21] in the future [22]. Since the entire comoving rest space will lie within an observer’s particle horizon eventually towards the past this World’s mass can be calculated readily as

$M = 2\pi^2R^3\rho = \frac1{\kappa c h_0} \frac{4\pi^2}{\sqrt{3 \Omega^0_\lambda}}.$

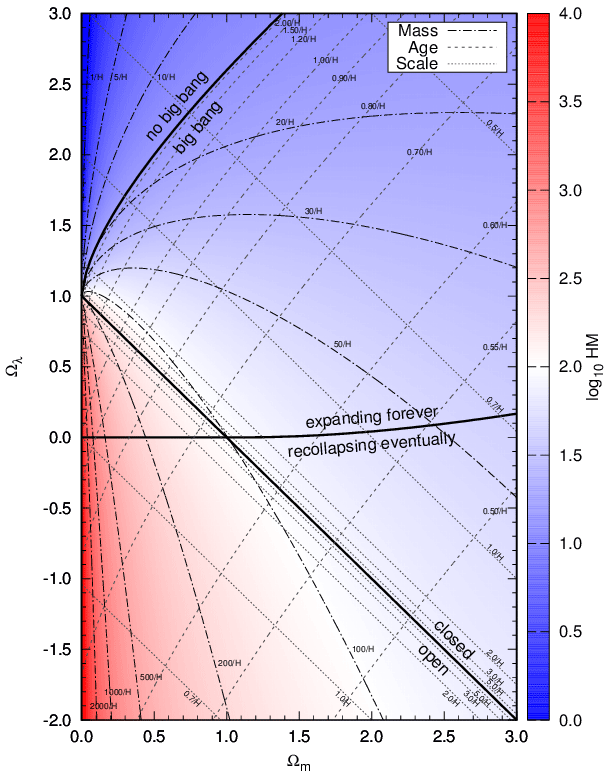
The results of this section can be visualized in the Omega diagram shown in figure 1. For convenience, it utilizes a sloppy parameter $H=h_0$ to scale times, $H=h_0/c$ to scale distances, and $H=\kappa c h_0$ to scale masses. The region denoted as recollapsing eventually contains the Robertson type O models, the region big bang and expanding forever the type M₁ models, and the region no big bang the type M₂ models. The A₁ and A₂ models are located along the line that separates the big bang and no big bang regions. The Einstein static universe is not in this picture because its Hubble parameter used for scaling vanishes. However, the Einstein–de Sitter universe is represented by the point with coordinates $\Omega_m=1,\ \Omega_\lambda=0$ on the line that separates the open and closed models. Its age equals $2/3/H$ and its mass $32\pi/H$ as seen in the previous section. For models with big bang the World’s age are obtained as [9]

$h_0 t_0 = \int_0^\infty \frac{dz}{(1+z)\sqrt{\Omega^0_m (1+z)^3 + \Omega^0_k (1+z)^2 + \Omega^0_\lambda}} = \frac23 \int_0^1 \frac{dy}{\sqrt{\Omega^0_m + \Omega^0_k y^{2/3} + \Omega^0_\lambda y^2}}$

with the integral with respect to the variable $y=(1+z)^{-3/2}$ again stated for possibly facilitating numerical evaluation.

Arbitrarily large masses are obtained in the vicinity of the axis $\Omega_m=0$ for $\Omega_\lambda \leq 1$ . It is apparent from figure 1 that in order to obtain an upper bound on the World’s mass a lower bound for both coordinates $\Omega_m$ and $\Omega_\lambda$ is needed. For the matter density Hubble’s estimate [13] from 1926 serves that purpose well. Together with his 1929 value [15] for $h_0$ one finds $\Omega_m \geq 10^{-4}$ . A possibility for constraining $\Omega_\lambda$ is to use the age of the universe. A Friedmann–Lemaître dust model with $\Omega_\lambda < -20$ is at most 0.3 Hubble times old, corresponding to less than one billion years assuming $h_0=500\,\mathrm{km/s/Mpc}$ . This is clearly unacceptable as already pointed out e.g. by A. Einstein [16]. The same is true even with today’s value of the Hubble constant for it would still just correspond to around 4 billion years. Therefore, calculating the World’s mass in a model with $\Omega_m=10^{-4},\ \Omega_\lambda=-20$ yields an upper bound of $10^7/H = 10^{58}\,\mathrm{kg}$ again with the 1929 value for the Hubble constant [15] corresponding to less than 10⁸⁵ hydrogen atoms, again not remotely what is claimed in table 1.

Conclusion

The considerations presented in this post demonstrate that it is not possible to find a Friedmann–Lemaître dust model that could reasonably account for the number of atoms as claimed in table 1 while being compatible with basic astronomical data. This applies both to data as known to Einstein as well as to more recent data. Therefore, not only the number of 10¹¹⁰ atoms in the universe as stated in table 1 seems to be wrong by some 30 orders of magnitude but also its attribution to A. Einstein. It appears inconceivable that he ever came up with such a number using any cosmological model that was considered viable in any sense.

PS: Just as an aside, if you took one of your favorite recent cosmological models with $h_0=67.3\,\mathrm{km/s/Mpc}$ and $\Omega_m=0.315,\ \Omega_\lambda=1-\Omega_m$ you would get a World’s mass of $135/H = 10^{54}\,\mathrm{kg}$ , out of which 16% is baryonic matter equivalent to quite exactly 10⁸⁰ hydrogen atoms.

PS2: If you are further inclined to numerology, you will likely compare the radius of the observable universe in your favorite recent cosmological model of $14.4\,\mathrm{Gpc}$ to the Bohr radius and will find that their quotient taken to the power of three equals six times 10¹¹⁰. You could therefore tend to claim that the volume of the observable universe is about 10¹¹⁰ times that of a hydrogen atom.

Some useless gibberish ...

Go, Lisp, and the World’s mass

Introduction

The Einstein static universe

Einstein–de Sitter universe

Friedmann–Lemaître models

Conclusion

References